Grids in Nature, Design and Generative Art

Grids have been used for centuries to transform ideas into tangible designs. They offer a simple, but effective framework, for organizing space and breaking down information into quantified units that we can more easily reckon with. As a generative artist who uses code as a medium, I rely on grids as foundational objects for building complex computational drawings. In this article, I’d like to explore how grids can be observed in both nature and culture, and how I use them for creative coding. By the end, I hope you will take a new perspective on the nature of grids, and gain practical insight for how grids are used in creative coding to make generative art.

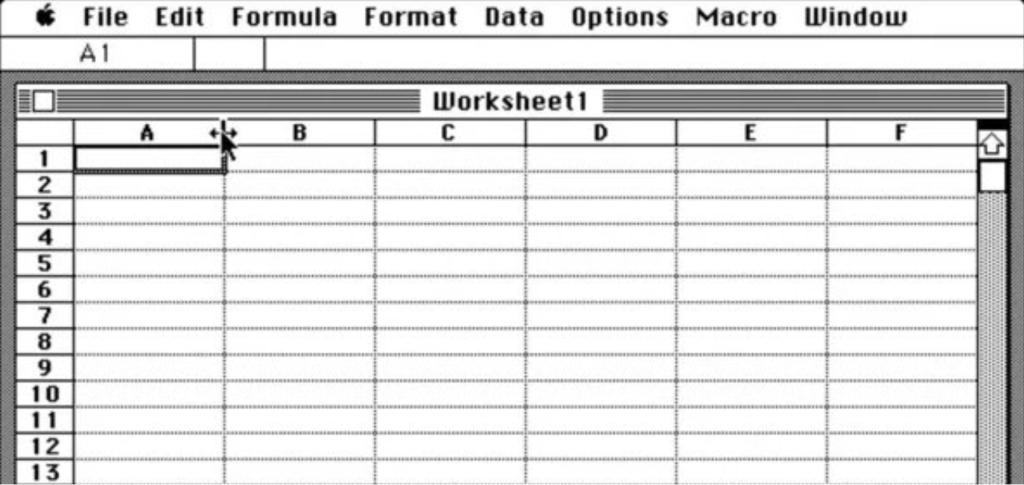
Have you ever used a spreadsheet? Spreadsheets are a prime example of the utility of grids; these are software tools that help us organize information, calculate data and solve problems. Before computers, hand-drawn tables were used to accomplish similar tasks. Over time, humans have been able to perform increasingly difficult tasks, using many forms of grids to design and think. Is this by chance? Maybe not. Looking closer, we find grids are at the very core of our nature.

The human brain includes a variety of specialized cells for doing computation. Scientists are learning more about the role of grid cells in the entorhinal cortex. Discovered in 2005, research suggests that grid cells are responsible for mapping “cognitive space”, allowing humans to mentally organize and store the complexities of both internal and external environments. [4]  From cells in our brains, to crystal formations, to the honey-comb arrangements of ommatidia in the compound eyes of insects–grids not only abound in nature, but within us.

Visit any modern city and you will be sure to experience grid-like thinking. Since ancient times city planners have used grids to layout urban developments. Mohenjo-daro was one of the world’s first major cities. Built around 2500 BC in modern day Pakistan, its remains reveal a well-planned street grid with an elaborate drainage system [6]. Archaeological records show every major metropolitan area–from Babylon to New York City–has relied on grid-like planning to layout urban space and design architecture.

In the mid-20th century, the Swiss-French Architect, Le Corbusier famously devised a grid system called the Modular. The idea is based on taking proportions and measurements from the height of an average person and dividing them based on the Fibonacci Sequence and Golden Ratio–mathematical patterns that have been observed widely in nature. The system was developed to create harmonious proportions and spaces that are both efficient and comfortable for human use.

Corbusier’s system was a continuation of a 2000-year-old search for the mathematical architecture of the universe, which captivated Pythagoras, Vitruvius, and Leonardo Da Vinci. This quixotic quest of anthropocentric fascination underscores an interesting point. Humans seem to use grids to enact an innate desire to divide and conquer space in proportion to themselves. Indeed, Corbusier’s Modular is considered significant because it puts the human form at the center of design (human-centered design), which has the large-scale effect of shaping our built world into grids [7].

 

Grids have also been central to many forms of visual art. Used since the Renaissance as a graphical component in painting, the aestheticization of grids came to prominence during the early 20th century in the Modernist movement. According to art historian Rosalind Krauss, the emergence of the grid was a crucial step in the evolution of modern art. In her well-known essay “Grids” published in 1979, Krauss notes that a structure which became the symbol of modernist artistic ambition first appeared in France, then in Russia and Holland, and has remained emblematic of modernism in visual arts ever since [8].

 

Agnes Martin (1912 – 2004) became known for using grids in the late 1950s, which marked a departure from representational painting. Her work foreshadowed Minimalism and influenced many other prominent artists, including Sol LeWitt (1928 – 2007) [9]. LeWitt eventually adopted the grid as a basic element of his work, using it to create precise and mathematical instructions for wall drawings and the production of abstract geometric sculptures [11].

Minimalism, with its emphasis on geometric abstraction and the use of basic forms, was significant in prefiguring the emergence of computer-generated art, which also utilized similar elements by relying on algorithms and precise geometric calculations. Thus, the use of grid patterns can be seen as a shared aesthetic between Minimalism and computer art.

Today, grids are a powerful tool for artists using code to create visual art. Similar to how a graphic designer might divide a canvas into fields for accurate alignment and organization of content, creative coders can use arrays and loops to build something analogous. Once established, the grid opens up countless creative possibilities to generate graphics that would be difficult to achieve by other methods. 

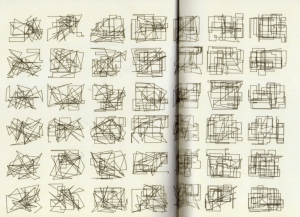
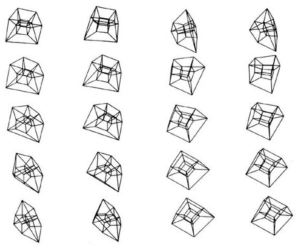
Let’s look at an example of how we might get started in code:

Create a square canvas
Divide the canvas into an equal set of rows and columns
Draw a line for each row and column

---

One key benefit of using a grid to produce art from code is that each cell can become a functional unit. Let’s start with a simple example. What if we simply wanted to rotate each cell? Once the grid is established it becomes trivial to compute a transformation.

Having the coordinates of each cell stored as variables means that we can easily draw shapes at those coordinates. For instance, we could loop through each of the cells, and draw a curve that is rotated to a randomly selected angle, divisible by quarter PI.

For each cell...
choose a random angle = PI/2 * random(between 1 and 4)
draw a quarter-arc at the center of the cell
rotated the arc to the random angle

---

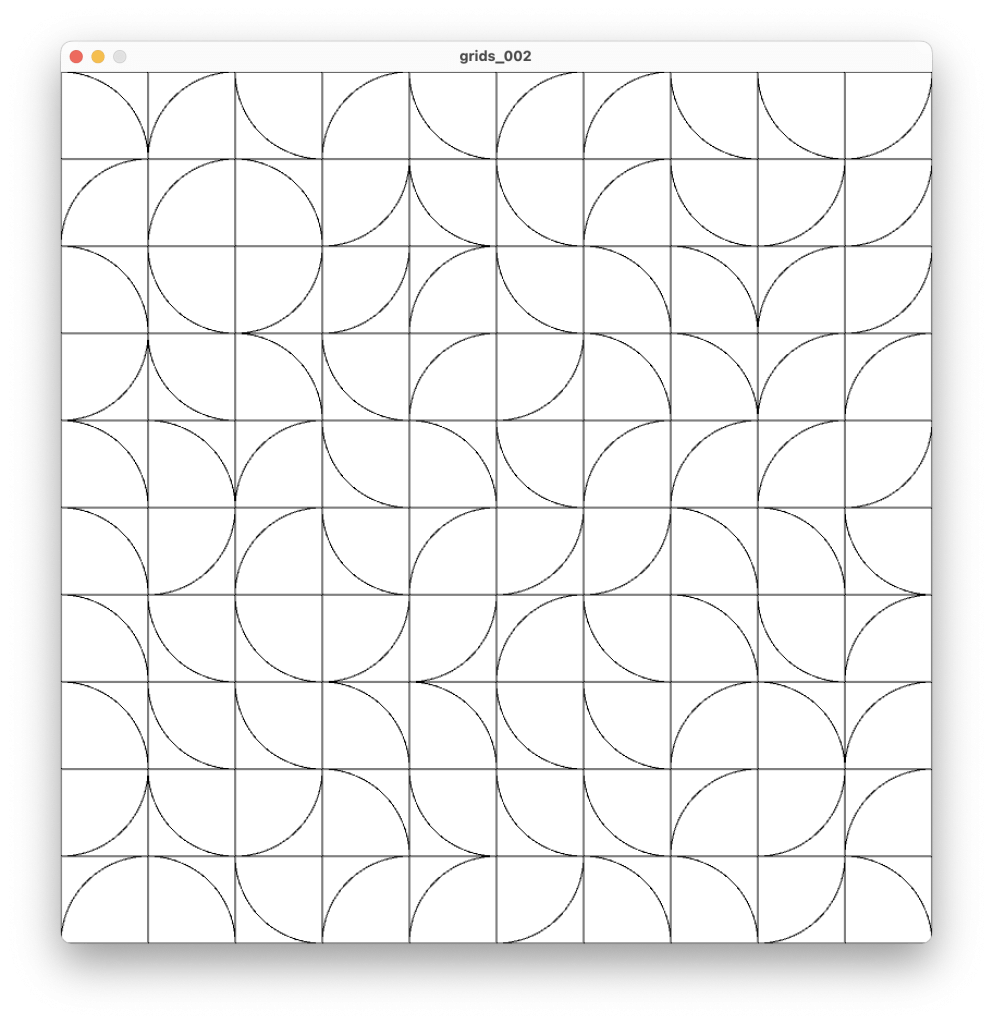
Until now, our examples have all resembled grids. Yet grids are just a starting point in creative coding. They’re not always about seeking the aesthetic of a grid. What’s key is that we can perform computation at every cell of the grid. For instance, we can use the coordinates of their centers to develop a field of values. Using these values, we can steer lines to draw curves that feel organic and natural.

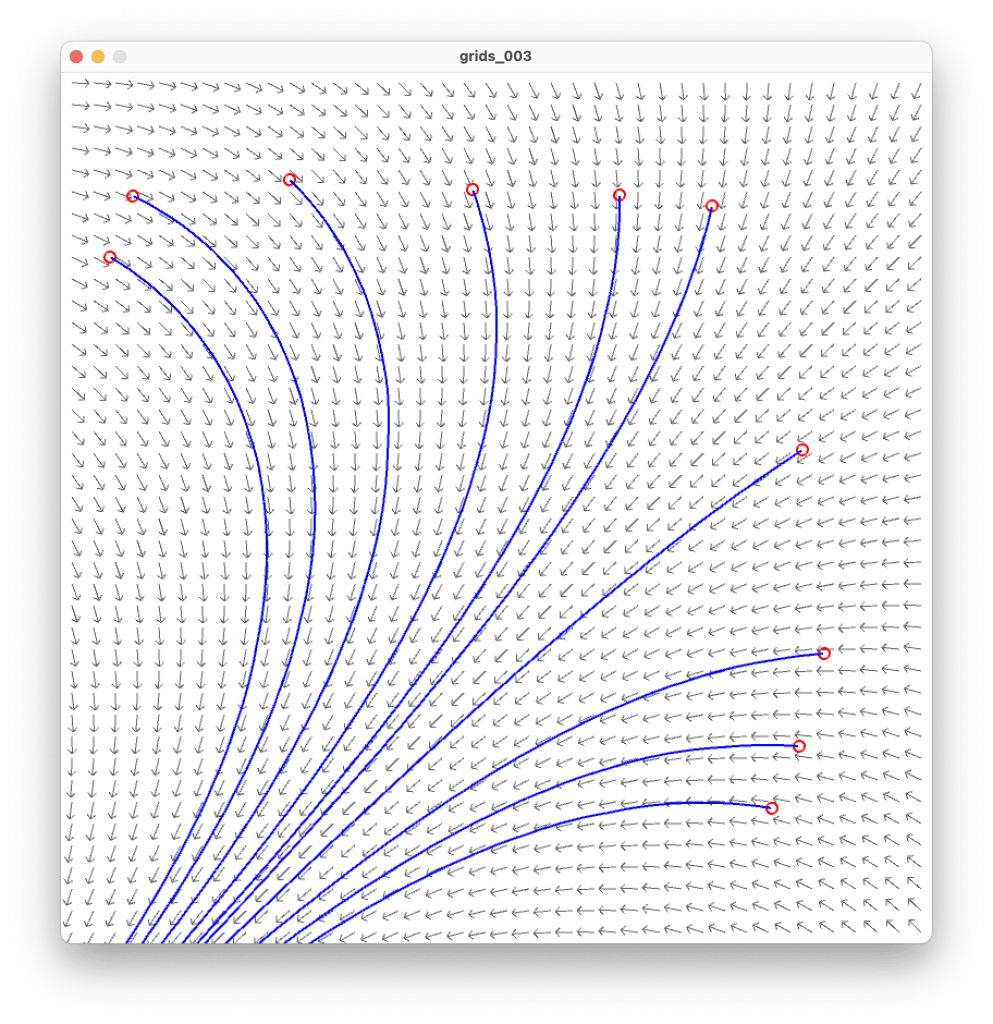
Vector fields, which are based on grids, are powerful tools for generating drawings from code. At each cell the value provides an angle, weight or force that directs the line’s stroke. When other techniques are applied, such as color, opacity and line-width, this method becomes incredibly convincing as an approach to generative drawing.

Let’s look at a video example of some code in action, where the angles inside each cell of a grid are being manipulated to steer the curves of a drawing. In this example, I’ve also exposed other variables as parameters to express the fluidity of this method of using the grid to draw algorithmically.

Of course, the examples above are just the tip of the iceberg! We can evolve generative drawings through additional techniques, such as change in color, weight and opacity of the lines. We can also evolve the mathematical expressions used for processing each vector coordinate across the grid. Final results can exceed our notion of there being any grid at all. In this way, grids become an invisible primitive foundation for the evolution of an aesthetic form, generated through computation.

Stemming from the simple idea of dividing space and information into quantified units, we can build complex systems of expression. From tiny organisms to giant civilizations, we find evidence of grids at work. It’s clear that grids play an essential role in our computerized world, in nature and in us. While artists have been using grids for centuries, the Modernist art movement adopted grids as a central motif. With digital machines and pixels, computer artists followed a natural predisposition to rely on grids. Today, as creative coders, we are building on this history in order to design systems that start from grids, but evolve into complex generative drawings.  Using code as a creative medium, grids unlock a vast world of possibilities.

REFERENCES

1. Staudigl, T., Leszczynski, M., Jacobs, J., Sheth, S.A., Schroeder, C.E., Jensen, O., and Doeller, C.F. (2018) Hexadirectional modulation of high-frequency electrophysiological activity in the human anterior medial temporal lobe maps visual space. Current Biology 28(20), 3443–3449.
2. Apple Computer Inc. (1981 ca). VisiCalc for Apple IIe (Computer). Courtesy of Apple Computer, Inc., 102630895. © Apple Computer, Inc.
3. WinworldPC. (2003). Microsoft Excel 1x. Retrieved from https://winworldpc.com/product/microsoft-excel/1x, [April 9, 2023]
4. Mathis, A., Stemmler, M.B., and Herz, A.V.M. (2015) Probable nature of higher-dimensional symmetries underlying mammalian grid-cell activity patterns. eLife 4:e05979
5. Monsalve-Mercado, M. M., & Leibold, C. (2017). Physical Review Letters.
6. Wikipedia. (2020). Mohenjo-daro. Retrieved from https://en.wikipedia.org/wiki/Mohenjo-daro, [April 9, 2023]
7. Le Corbusier. The Modulor. Translated by Peter de Francia and Anna Bostock, MIT Press, 2011. 2nd ed. (Original work published 1942)
8. Krauss, R. (1979). Grids. October, 9(Summer), 50-64. The MIT Press. Retrieved from http://www.jstor.org/stable/778321 [Accessed April 22, 2023].
9. McConnell, Alison. (2015) Living on (and off) the Grid. Wall Street Journal. July 24, 2015. https://www.wsj.com/articles/living-on-and-off-the-grid-1437768845.
10. Tate Modern. “Agnes Martin,” 3 JUNE – 11 OCTOBER 2015. Accessed on April 15, 2023, https://www.tate.org.uk/whats-on/tate-modern/agnes-martin.
11. Fabrizi, M. (2016, June 15). “Irrational Thoughts Should be Followed Absolutely and Logically”: Sol LeWitt’s “Variations of Incomplete Open Cubes” (1974). Socks. Retrieved from https://socks-studio.com/irrational-thoughts-should-be-followed-absolutely-and-logically [April 22, 2023].
12. Nees, Georg. “Computergrafik” (1966). Exhibitions of Graphic Works Algorithmically Generated by a Digital Computer at Siemens Company, Erlangen (Germany). Accessed from http://dada.compart-bremen.de/item/exhibition/164.
13. Burns, Thomas Elliott. (2014). Early computer art. Accessed from https://www.burns-office.com/2014/12/03/research/lecture/early-computer-art/.
14. Mansion, M. (2023). Flow Field sketches using Processing: An Open Source Creative Coding Framework by Processing.org